问题
填空题
已知多项式2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3是二次多项式,则a2+b2= 。
答案
13
专题:计算题;方程思想.
分析:根据多项式的次数的定义,可知此多项式中次数最高的项的次数为二,即高于二次的项的系数为0.故本题可先将多项式2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3合并同类项,再分别令四次项系数、三次项系数为0,得出关于a、b的二元一次方程组,解此方程组求出a、b的值,然后代入即可得到a2+b2的值.
解答:解:∵2ax4+5ax3-13x2-x4+2021+2x+bx3-bx4-13x3=(2a-b-1)x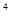 +(5a-13+b)x
+(5a-13+b)x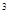 -13x
-13x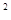 +2x+2021,
+2x+2021,
又∵此多项式为二次多项式,
∴ ,
,
解得 .
.
所以a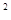 +b
+b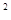 =2
=2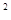 +3
+3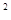 =13.
=13.
故答案为13.
点评:本题主要考查了多项式的次数的定义:多项式中次数最高的项的次数叫做多项式的次数.一个多项式的次数为二次,即此多项式中高于二次的项的系数为0.本题根据多项式的次数的定义,得出四次项系数、三次项系数都为0是解题的关键.
