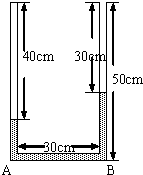
一根截面积均匀粗细不计的U形管两侧长度均为50cm,水平部分长度为30cm,且左侧管口封闭,右侧管口敞开,如图所示.管内灌有水银,左边水银上方的空气柱长度为40cm,右边水银面离管口30cm.(大气压强为75cmHg,环境温度为27°C)
(1)若将U形管绕其水平部分AB缓慢旋转180?,试分析说明管中的水银是否流出.若不流出请说明理由;若流出,请计算管中水银流出多少厘米?
(2)若往右管中加入10cm水银柱后,为了保持左管气柱长度不变,则环境温度要升高到多少?
(3)若改变环境温度使左右两管水银面相平,求环境温度的改变量.
(1)漏出水银
设右侧还剩有xcm水银柱,以左侧封闭气体做为研究对象,
则右侧开口向上时封闭气体的压强为P1=75+10cmHg,管内水银的高度为x,
右侧开口向下时封闭气体的压强为P2=75-x(cmHg),
由于环境的温度保持不变,故封闭气体发生等温变化,
由p1V1=p2V2则有(75+10)40=(75-x)(130-x),
即x2-205x+6350=0,x=38cm,
可见管中水银流出Y=30+20+10-38=22cm;
(2)在往右管中加入10cm水银柱后,要保持左管气柱长度不变,故封闭气体发生了等容变化,则由查理定律:
=P1 T1 P3 T3
可得
=75+10 300
,75+20 T3
解得环境的温度要升高到T3=335.29K
(3)当左右两管水银面相平时封闭气体的压强等于外界大气的压强,则封闭气体的长度变为35cm,由理想气体状态方程
=P1V1 T1 P4V4 T4
可得
×40=75+10 300
,35×75 T4
即T4=231.6K,
环境温度降低了△t=300-231.6=68.4°C.
