问题
计算题
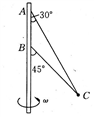
如图所示,用两条绳子系住一个质量m=0.1kg的小球,上面绳长l=2m,两条绳子都拉直时与转轴夹角分别为30°与45°,问
(1)小球的角速度在什么范围内,两条绳子可以始终拉紧?
(2)当角速度为3 rad/s时,上、下两条绳子的拉力分别是多大?
答案
解:(1) 设BC恰好拉直时(F2=0 ),角速度为ω1 ,
则有F1cos30 °=mg
F1sin 30 °=m ω12/sin30 °,
解得ω1=2.4rad/s.
当ω大到一定程度时,AC仍然拉直,但F1已为0,设此时的角速度为ω2,
则有F2 cos 45 °=mg
F2sin45 °=m ω22/sin 30 °,
得ω2=3.16rad/s.
所以要使两绳始终拉紧,必须满足2.4rad/s ≤ω≤3.16 rad/s.
(2) 当ω=3rad/s 时,F1 ,F2 同时存在,
所以 F1sin30 °+F2sin45 °=m ω2 Lsin 30 °
F1cos 30 °+F2cos 45 °=mg,
解得F1=0.27 N
F2 =1.09 N
