问题
计算题
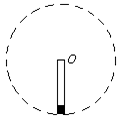
如图所示，在内壁光滑的平底试管内放一个质量为m=10g的小球（可视为质点），试管的开口端加盖与水平轴O连接，试管底与O相距为L=10cm，试管在转轴带动下沿竖直平面做匀速圆周运动．g取10m/s2．求：
(1)转轴的角速度满足什么条件时，小球不会脱离试管底？
(2)当转轴的角速度为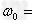
30rad/s时，小球到达最高点时对试管底的压力．
答案
解：(1)对小球，在最高点时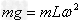
解得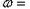
10rad/s
因此，转轴的角速度ω≥10rad/s时，小球不会脱离试管底
(2)对小球，在最高点时，设试管底对小球的弹力为N
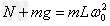
解得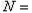
0.8N
由牛顿第三定律得，小球对试管底的压力
0.8N，方向竖直向上