问题
计算题
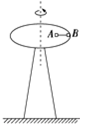
如图所示，水平转台高1.25 m，半径为0.2 m，可绕通过圆心处的竖直转轴转动．转台的同一半径上放有质量均为0.4 kg的小物块A、B(可看成质点)，A与转轴间距离为0.1 m，B位于转台边缘处，A、B间用长0.1 m的细线相连，A、B与水平转台间最大静摩擦力均为0.54 N，g取10 m/s2。
(1)当转台的角速度达到多大时细线上出现张力？
(2)当转台的角速度达到多大时A物块开始滑动？
(3)若A物块恰好将要滑动时细线断开，此后转台保持匀速转动，求B物块落地瞬间A、B两物块间的水平距离．(不计空气阻力，计算时取π＝3)
答案
解：(1)由Ff＝mω2r可知，B先达到临界状态，故当满足Ffm<mω12r时线上出现张力
解得ω1＝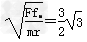
rad/s
(2)当ω继续增大，A受力也达到最大静摩擦力时，A开始滑动
Ffm－FT＝mω′2r/2
Ffm＋FT＝mω′2r
得ω′＝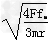
=3 rad/s
(3)细线断开后，B沿水平切线方向飞出做平抛运动
由h＝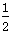
gt2得t＝0.5 s
vB＝ωr＝0.6 m/s
可得B的水平射程xB＝vBt＝0.3 m
细线断开后，A相对静止于转台上，t时间转过角度θ＝ωt＝1.5 rad即90°
故AB间水平距离lx＝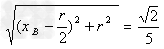
=0.28 m（0.3均可）