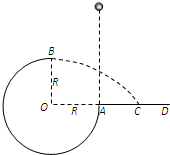
如图7所示,竖直平面内的
圆弧形光滑轨道半径为 R,A 端与圆心 O 等高,AD 为水平面,B 点为光滑轨道的最高点且在O 的正上方,一个小球在 A 点正上方某处由静止释放,自由下落至 A 点进入圆轨道并知通过 B 点时受到轨道的弹力为mg(从A点进入圆轨道时无机械能损失),最后落到水平面 C 点处.求:3 4
(1)释放点距 A 点的竖直高度 h和落点 C 到 A 点的水平距离x;
(2)如果将小球由h=R处静止释放,请问小球能否通过最高点B点,如果不能通过,请求出脱离圆轨道的位置E与O的连线与竖直方向夹角的正弦值.
(1)小球通过最高点B时,由牛顿第二定律,有:
mg+FN=mvB2 R
又FN=mg
解得:vB=2gR
设释放点到A点高度为h,小球从释放到运动至B点的过程中,
根据动能定理,有:mg(h-R)=
mvB21 2
解得:h=2R,
由平抛规律:R=
gt21 2
x=vBt,
联立解得x=2R,所以C点距A点距离:△x=2R-R=R
即释放点距A点的竖直高度h为2R,落点C到A点的水平距离为R.
(2)小球到达B点时最小速度为v,有:mg=mv 2 R
若能到达最高点应满足mgR=
mv2+mgR,显然不可能成立,即不能到最高点.1 2
设到最高点E的速度为vE,
E与O的连线与竖直方向夹角θ,由动能定理有:mgR(1-cosθ)=
mvE2…①,1 2
在E点脱离轨道时有:mgcosθ=m
…②vE2 R
联立①②解得:cosθ=2 3
所以:sinθ=5 3
答:(1)释放点距 A 点的竖直高度 h和落点 C 到 A 点的水平距离为R;
(2)如果将小球由h=R处静止释放,小球不能通过最高点B点,小球脱离圆轨道的位置E与O的连线与竖直方向夹角的正弦值为
.5 3
