问题
计算题
在质量为M的电动机上，装有质量为ｍ的偏心轮，偏心轮转动的角速度为ω，当偏心轮重心在转轴正上方时，电动机对地面的压力刚好为零；则偏心轮重心离转轴的距离多大? 在转动过程中，电动机对地面的最大压力多大?
答案
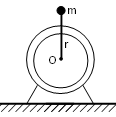
解：设偏心轮的重心距转轴ｒ
偏心轮等效为用一长为ｒ的细杆固定质量为ｍ（轮的质量）的质点，绕转轴转动
轮的重心在正上方时，电动机对地面的压力刚好为零
则此时偏心轮对电动机向上的作用力大小等于电动机的重力
即：F=Mｇ①
根据牛顿第三定律，此时轴对偏心轮的作用力向下
大小为F=M ｇ
其向心力为：F+mg=m ω2r ②
由①②得偏心轮重心到转轴的距离为：
r= （M+m）g/ （mω2） ③
当偏心轮的重
心转到最低点时，电动机对地面的压力最大
对偏心轮有：F'-mg=mω2r ④
对电动机，设它所受支持力为FN，FN=F'+Mg ⑤
由③、④、⑤解得FN=2（M+m）g
由牛顿第三定律得，电动机对地面的最大压力为2（M+m）g