问题
选择题
如图所示,一根长为L的轻质细线,一端固定于O点,另一端拴有一质量为m的小球,可在竖直的平面内绕O点摆动,现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时的速度是( )
A.5gL 2
B.5gL 2
C.3gL
D.3gL 2 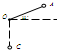
答案
对小球进行受力分析及运动过程分析如下图所示.
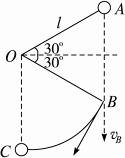
从静止释放小球,细线松弛,小球只受重力做自由落体运动,下落到A与水平面的对称点B时细线将张紧,
根据自由落体运动的规律
则vB=
方向竖直向下.2gL
在B位置细线突然张紧,对小球施以冲量,使小球竖直向下的速度变为沿圆弧切线方向上的速度,vB′=vBcos30°,
小球的动能在瞬间减少,根据功能关系只能是绳子突然张紧“爆发”做功使机械能部分变为其他形式的能量(声能、内能等).
小球由B运动至C,绳子的拉力与运动方向垂直不做功,只有重力做功,机械能守恒.
此过程中,重力势能减少量△Ep=mgl(1-cos60°)
动能的增加量△Ek=
mvC2-1 2
mv′B21 2
有mgl(1-cos60°)=
mvC2-1 2
mv′B21 2
代入vB′=vBcos30°=
cos30°2gL
得vC=
.5gL 2
故选A.
