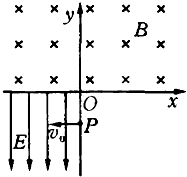
如图所示,在xOy平面内的第Ⅲ象限中有沿-y方向的匀强电场,场强大小为E.在第I和第II象限有匀强磁场,方向垂直于坐标平面向里.有一个质量为m,电荷量为e的电子,从y轴的P点以初速度v0垂直于电场方向进入电场(不计电子所受重力),经电场偏转后,沿着与x轴负方向成45°角进入磁场,并能返回到原出发点P.
(1)并画出电子运动轨迹的示意图;
(2)求P点距坐标原点的距离
(3)电子从P点出发经多长时间再次返回P点.
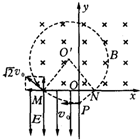
(1)如右图所示,电子进入电场,从P点到M点做类平抛运动,进入磁场后做匀速圆周运动,离开磁场后从N点到P点做匀速直线运动,画出轨迹如图所示.
(2)电子在电场中运动过程,有vy=v0=
teE m
解得,t=mv0 eE
则得
=. OP
?1 2
t2=eE m m v 20 2eE
(3)电子在电场中运动时间为t1=t=mv0 eE
电子在磁场中运动时间为t2=
T=3 4
?3 4
=2πm eB 3πm 2eB
电子从N点到P点的距离为:
=. NP
?2 . OP
电子在磁场中运动的速率为v=
v02
则电子从N点到P点的时间为t3=
=. DP v mv0 2eE
故总时间为t总=t1+t2+t3=
+3mv0 2eE 3πm 2eB
又由图知,OM=v0t1=
,ON=m v 20 eE
=. OP m v 20 2eE
而MN=OM+ON=
R,2
联立上两式得,电子在磁场中运动的轨迹半径R=3m v 20 2
eE2
又evB=mv2 R
解得,B=4E 3v0
所以t总=
+3mv0 2eE
=(4+3π)3πm 2eB 3mv0 8eE
答:
(1)画出电子运动轨迹的示意图如图所示;
(2)P点距坐标原点的距离为
.m v 20 2eE
(3)电子从P点出发经(4+3π)
的时间再次返回P点.3mv0 8eE
