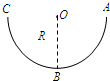
如图所示,竖直平面上有一光滑绝缘半圆轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,轨道的半径为R.一个质量为m的带正电的小球从槽右端的A处无初速沿轨道下滑,滑到最低点B时对槽底压力为2mg.求小球在滑动过程中的最大速度.
两位同学是这样求出小球的最大速度的:
甲同学:B是轨道的最低点,小球过B点时速度最大,小球运动过程机械能守恒,mgR=
mv2,解得小球在滑动过程中的最大速度为v=1 2
.2gR
乙同学:B是轨道的最低点,小球过B点时速度最大,小球在B点受到轨道的压力为FN=2mg,由牛顿第二定律有FN-mg=m
,解得球在滑动过程中的最大速度v=v2 R
.gR
请分别指出甲、乙同学的分析是否正确,若有错,将最主要的错误指出来,解出正确的答案,并说明电场的方向.
甲同学的分析是错误的,小球的机械能不守恒.
乙同学分析也是错误的,小球在滑动过程中的最大速度的位置不在最低点B.
正确解如下:
小球在B点时,FN-mg=mv2 R
∵FN=2mg∴v2=gR
从A到B,设电场力做功WE,由动能定理,WE+mgR=
mv21 2
得WE=-
mgR1 2
∵电场力做负功,∴带电小球受电场力方向向右FE=
=WE R
mg1 2
场强方向向右
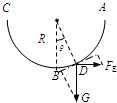
从A到B之间一定有位置D是小球运动的切线方向瞬时合力为零处,也是小球速度最大处
设OD连线与竖直方向夹角θ,FEcosθ=Gsinθ
m1 2
=mgRcosθ-FE(R-Rsinθ)v 2max
vmax=
)gR(
-15
答:电场方向向右,最大速度为vmax=
.gR(
-1)5
