如图所示,在地面附近有一范围足够大的互相正交的匀强电场和匀强磁场.匀强磁场的磁感应强度为B,方向水平并垂直纸面向外,一质量为m、带电量为-q的带电微粒在此区域恰好做速度大小为v的匀速圆周运动.(重力加速度为g)
(1)求此区域内电场强度的大小和方向;
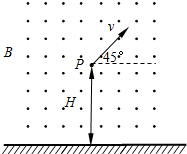
(2)若某时刻微粒运动到场中距地面高度为H的P点,速度与水平方向成450,如图所示.则该微粒至少须经多长时间运动到距地面最高点?最高点距地面多高?
(3)在(2)问中微粒运动P点时,突然撤去磁场,同时电场强度大小不变,方向变为水平向右,则该微粒运动中距地面的最大高度是多少?

(1)带电微粒在做匀速圆周运动,电场力与重力应平衡,有mg=Eq,即E=
,方向竖直向下.mg q
(2)粒子做匀速圆周运动,轨道半径为R,如图所示.qvB=m
,v2 R
根据几何关系可确定,最高点与地面的距离为Hm=H+R(1+cos450),
解得Hm=H+
(1+mv Bq
).2 2
该微粒运动周期为T=
,2πm Bq
根据运动圆弧对应的圆心角,可得粒子运动至最高点所用时间为t=
T=3 8
.3πm 4Bq
(3)设粒子上升高度为h,由动能定理得-mgh-Eqhcot450=0-
mv2,1 2
解得h=
=mv2 2(mg+Eq)
.v2 4g
微粒离地面最大高度为H+
.v2 4g
答:(1)求此区域内电场强度的大小
和方向为竖直向下;mg q
(2)该微粒至少须经
时间运动到距地面最高点;最高点距地面高度为Hm=H+3πm 4Bq
(1+mv Bq
)2 2
(3)该微粒运动中距地面的最大高度是H+
.v2 4g
