问题
计算题
（16分）如图所示，一轻弹簧的下端固定在倾角θ＝37°的斜面上，上端连一不计质量的挡板．一质量m＝2 kg的物体从斜面上的A点以初速度v0＝
m/s下滑。A点距弹簧上端B的距离AB＝4 m，当物体到达B后将弹簧压缩到C点，最大压缩量BC＝0.2 m，然后物体又被弹簧弹上去，弹到的最高位置为D点，D点距A点AD＝3 m。g取10 m/s2，求：
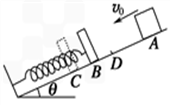
(1)物体与斜面间的动摩擦因数μ；
(2)弹簧的最大弹性势能Epm。
答案
0.5 24J
题目分析：解：(1)整个过程从A到D，由系统能量转化与守恒定律有：
mgssin37°-umgcos37°L=0-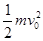
其中s=3m，L=5.4m
代入数据计算得μ=0.5
(2)弹簧压缩到C点时，对应的弹性势能最大，由A到C的过程：由系统能量转化与守恒定律有：
Epm=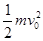+mgL1sin37°-μmgcos37°L1 其中L1=4.2m
代入数据计算得Epm＝24J