问题
问答题
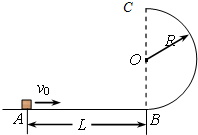
如图所示,水平不光滑轨道AB与半圆形光滑的竖直圆轨道BC相连,B点与C点的连线沿竖直方向,AB段长为L,圆轨道的半径为R.一个小滑块以初速度v0从A点开始沿轨道滑动,已知它运动到C点时对轨道的压力大小恰好等于其重力,求
(1)滑块在C点时的速度.
(2)滑块与水平轨道间的动摩擦因数.
(3)滑块离开C点至着地时的水平射程.
答案
(1)由题意知,在C点滑块做圆周运动的向心力:
F=mg+N=mg+mg=2mg,
由牛顿第二定律得:2mg=m
,解得:vc=v 2c R
;2gR
(2)从A到C过程中,由动能定理得:
-μmgL-mg?2R=
mvC2-1 2
mv02,1 2
解得:μ=
;
-6gRv 20 2gL
(3)滑块离开轨道后做平抛运动,
竖直方向:2R=
gt2,1 2
水平方向:s=vCt,
解得:s=
R;8
答:(1)滑块在C点时的速度为
.2gR
(2)滑块与水平轨道间的动摩擦因数
.
-6gRv 20 2gL
(3)滑块离开C点至着地时的水平射程
R.8
