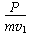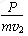问题
问答题
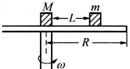
如图所示,一圆盘可以绕其竖直轴在水平面内运动,圆柱半径为R,甲、乙两物体的质量分别为M和m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用长为L的轻绳连在一起,L<R.若将甲物体放在转轴位置上,甲、乙连线正好沿半径方向拉直.问:
(1)当轻绳恰好产生力的瞬间,此时圆盘旋转的角速度为多大?
(2)要使两物体与圆盘不发生相对滑动,则圆盘旋转的角速度最大不得超过(两物体看作质点)
答案
轻绳恰好产生力的瞬间,绳子的弹力等于0,乙物体达到最大静摩擦力,此时对乙物体有:
最大静摩擦力提供向心力
mω2L=μmg
解得:ω=μg L
当绳子的拉力等于A的最大静摩擦力时,角速度达到最大且不发生相对滑动,
有T+μmg=mLω2,T=μMg.
所以ω=μ(M+m)g mL
答:(1)当轻绳恰好产生力的瞬间,此时圆盘旋转的角速度为
;μg L
(2)要使两物体与圆盘不发生相对滑动,则圆盘旋转的角速度最大不得超过
(两物体看作质点).μ(M+m)g mL