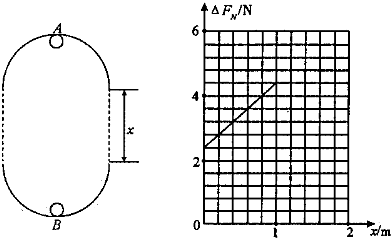
如图所示,在同一竖直平面内两正对着的半径为R的相同半圆滑轨道,相隔一定的距离x,虚线沿竖直方向,一质量为m的小球能在其间运动.今在最低点B与最高点A各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来.当轨道距离x不同时,测得两点压力差△FN与距离x的图象如右图所示.(不计空气阻力,g取10m/s2
(1)当x=R时,为使小球不脱离轨道运动,求小球在B点的最小速度(用物理量的符号表示)
(2)试写出A、B两点的压力差△FN与 x的函数关系.(用m、R、g表示)
(3)根据图象,求小球的质量和轨道半径.
(1)小球恰能在A点沿轨道运动时:
mg=mv 2A R
此时,小球在B点动能最小,由机械能守恒:
mvB2=mg3R+1 2
mvA2 1 2
解得:vB=7gR
(2)在B点:FNB-mg=mv 2B R
在A点:FNA+mg=mv 2A R
小球从A到B机械能守恒:
mvB2=mg(2R+x)+1 2
mvA2 1 2
两点的压力差:△FN=FNB-FNA=6mg+2mgx R
(3)由图象知:
截距:6mg=2.4
m=0.04kg
斜率:k=
=22mg R
R=0.4m
答:(1)B点的最小速度为
; (2)两点压力差的绝对值为6mg+7gR
;(3)小球的质量为0.04kg;半径为0.4m.2mgx R
