问题
问答题
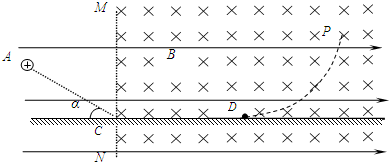
如图所示,空间内存在水平向右的匀强电场,在虚线MN的右侧有垂直纸面向里、磁感应强度为B的匀强磁场,一质量为m、带电荷量为+q的小颗粒自A点由静止开始运动,刚好沿直线运动至光滑绝缘的水平面C点,与水平面碰撞的瞬间小颗粒的竖直分速度立即减为零,而水平分速度不变,小颗粒运动至D处刚好离开水平面,然后沿图示曲线DP轨迹运动,AC与水平面夹角α=30°,重力加速度为g.求:
(1)匀强电场的场强E.
(2)AD之间的水平距离d.
(3)已知小颗粒在轨迹DP上某处的最大速度为vm,该处轨迹的曲率半径是距水平面高度的k倍,则该处的高度为多大?
答案
(1)小球受力如图所示:

qE=mgcotα 解得:E=
mg3 q
(2)设小球在D点速度为vD,小球在D点离开水平面的条件是:qvDB=mg
得到vD=mg qB
由于小球与水平面碰撞的瞬间小颗粒的竖直分速度立即减为零,而水平分速度不变.
根据动能定理,得
qEd=
m1 2 v 2D
得d=
m2g3 6q2B2
(3)当速度方向与电场力和重力合力方向垂直时,即当洛伦兹力与重力和电场力的合力共线时,速度最大.
则:qvmB-
=mmg sin30° v 2m R
又R=kh
解得:h=k
.m v 2m qBvm-2mg
