问题
问答题
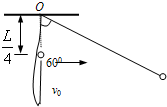
长为L的轻绳一端系于固定点O,另一端系质量为m的小球.将小球从O点正下方
处,以一定初速度水平向右抛出,经一定时间绳被拉直以后,小球将以O为支点在竖直平面内摆动.已知绳刚被拉直时,绳与竖直线成60°角,如图所示,L 4
(1)求:小球水平抛出时的初速度v0
(2)在绳被拉紧的瞬间,小球立即做圆周运动;求小球摆到最低点时,绳所受拉力T.
答案
(1)小球在绳被拉直前作平抛运动,设小球抛出后经时间t绳被拉直,则:
水平位移为:x=Lsin60°=v0t
竖直高度为:h=lcos60°-
=L 4
gt21 2
由此解得:t=L 2g
v0=1 2 6gL
(2)在绳被拉直前瞬间,小球速度的水平分量为v0,竖直分量为gt,速度大小为:
v=
=v02+(gt)2 2gL
速度与竖直方向的夹角为φ:则tanφ=
=v0 vy 3
所以,φ=60°
可见小球速度与绳沿同一线,小球动量在绳拉力的冲量作用下减为零,以后小球作摆动,由机械能守恒定律可知小球到最低点时:
mv′2=mgL(1-cos60°)1 2
设在最低点时绳子对物体的拉力为T,由牛顿第二定律得:
T-mg=mv′2 L
解得:T=2mg
答:(1)小球水平抛出时的初速度为1 2
;6gL
(2)小球摆到最低点时,绳所受拉力为2mg.
