如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)、一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°.下列说法中正确的是( )
A.电子在磁场中运动的时间为πL v0
B.电子在磁场中运动的时间为2πL 3v0
C.磁场区域的圆心坐标为(
,
L3 2
)L 2
D.电子在磁场中做圆周运动的圆心坐标为(0,-2L)
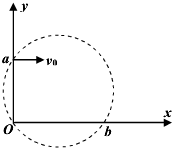
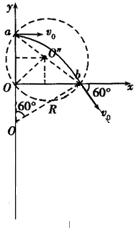
A、B、电子的轨迹半径为R,由几何知识,Rsin30°=R-L,得R=2L
电子在磁场中运动时间t=
,而 T=T 6
,得:t=2πR v0
,故A错误,B正确;2πL 3v0
C、设磁场区域的圆心坐标为(x,y)其中 x=
Rcos30°=1 2
L y=3 2 L 2
所以磁场圆心坐标为 (
L,3 2
),故C正确;L 2
D、根据几何三角函数关系可得,R-L=Rcos60°,解得R=2L
所以电子的圆周运动的圆心坐标为(0,-L),故D错误;
故选:BC
