问题
问答题
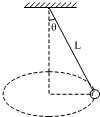
在如图所示的圆锥摆中，已知绳子长度为L，绳子转动过程中与竖直方向的夹角为θ，求小球做匀速圆周运动的周期．
答案
如图小球的受力如右图所示
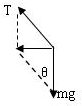
，由牛顿第二定律得：
mgtanθ=m
| 4π2r |
| T2 |
由图可知，小球圆周运动的半径：r=Lsinθ
联立解得：T=2π
|
|
|
答：小球做匀速圆周运动的周期T=2π
|
搜题请搜索小程序“爱下问搜题”
在如图所示的圆锥摆中，已知绳子长度为L，绳子转动过程中与竖直方向的夹角为θ，求小球做匀速圆周运动的周期．
如图小球的受力如右图所示
，由牛顿第二定律得：
mgtanθ=m
| 4π2r |
| T2 |
由图可知，小球圆周运动的半径：r=Lsinθ
联立解得：T=2π
|
|
|
答：小球做匀速圆周运动的周期T=2π
|