问题
选择题
在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（ ）
A．（a-b）2=a2-2ab+b2
B．（a+b）2=a2+2ab+b2
C．a2-b2=（a+b）（a-b）
D．a2+ab=a（a+b）
答案
答案：C
解：正方形中，S阴影=a2-b2；
梯形中，S阴影=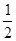
（2a+2b）（a-b）=（a+b）（a-b）；
故所得恒等式为：a2-b2=（a+b）（a-b）．
故选C