问题
问答题
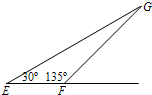
如图,纸面内有E、F、G三点,∠GEF=30°,∠EFG=135°.空间有一匀强磁场,磁感应强度大小为B,方向垂直于纸面向外.先使带有电荷量为q(q>0)的点电荷a在纸面内垂直于EF从F点射出,其轨迹经过G点;再使带有同样电荷量的点电荷b在纸面内与EF成一定角度从E点射出,其轨迹也经过G点.两点电荷从射出到经过G点所用的时间相同,且经过G点时的速度方向也相同.已知点电荷a的质量为m,轨道半径为R,不计重力.求:
(1)点电荷a从射出到经过G点所用的时间;
(2)点电荷b的速度大小.
答案
解;设点电荷a的速度为v,由牛顿第二定律得:qvB=mv2 R
解得:v=
①qRB m
设点电荷a作圆周运动的周期为T,则:T=
②2πR v
点电荷运动轨迹如图所示:
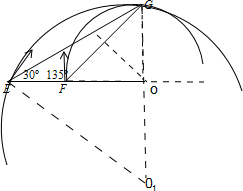
设点电荷a从F点进入磁场后的偏转角为θ
由几何关系得:θ=90° ③
故a从开始运动到经过G点所用时间t=
T=90 360
T 1 4
①②③联立得:t=
④πm 2qB
(2)设点电荷b的速度大小为v1,轨道半径为R1,b在磁场中偏转角为θ1,
由题意得:t=
=R1θ1 v1
⑤Rθ v
解得:v1=
v ⑥R1θ1 Rθ
由于两轨道在G点相切,所以过G点的半径OG和O1G在同一条直线上,
由几何关系得:θ1=60° ⑦
R1=2R ⑧
②③⑥⑦⑧联立得:v1=4qBR 3m
答:(1)点电荷a从射出到经过G点所用的时间t=
;πm 2qB
(2)点电荷b的速度大小v1=
.4qBR 3m
