问题
多选题
如图所示,铁路在弯道处的内外轨道高低是不同的,已知内外轨道对水平面倾角为θ,弯道处的圆弧半径为R,质量为m的火车转弯下列说法正确的是( )
A.若速度小于
则这时内轨对内侧车轮轮缘有挤压Rgtanθ
B.若速度等于
则这时铁轨和车轮轮缘间无挤压Rgtanθ
C.若速度等于
则这时铁轨对火车的支持力等于mg/cosθRgtanθ
D.若速度小于Rgtanθ则这时铁轨对火车的支持力大于mg/cosθ 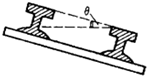
答案
火车以某一速度v通过某弯道时,内、外轨道均不受侧压力作用,其所受的重力和支持力的合力提供向心力
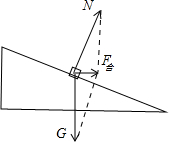
由图可以得出
F合=mgtanθ(θ为轨道平面与水平面的夹角)
合力等于向心力,故
mgtanθ=mv2 R
解得v=
.gRtanθ
A、若速度小于
,则重力和支持力提供的合力大于向心力,所以内轨对内侧车轮轮缘有挤压.故A正确.Rgtanθ
B、若速度等于
则这时铁轨和车轮轮缘间无挤压.故B正确.Rgtanθ
C、若速度等于
,竖直方向上合力为零,有Ncosθ=mg,解得N=Rgtanθ
.故C正确.mg cosθ
D、若速度小于
,内轨对内侧车轮轮缘有挤压,挤压力斜向上,则铁轨对火车的支持力小于Rgtanθ
.故D错误.mg cosθ
故选ABC.
