问题
填空题
5个大小不同的圆的交点最多有______个.
答案
画2个圆,最多有2个交点,可以写成2×(2-1)个交点;
画3个圆,最多有6个圆,可以写成3×(3-1)个交点;
画4个大小不同的圆,最多有12个交点,可以写成是4×(4-1)个交点;…
所以画n个圆时,最多有n(n-1)个交点,
当n=5时,交点最多有:5×(5-1)=20(个),如图;
答:画7个大小不同的圆,最多有20个交点.
故答案为:20.
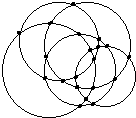
5个大小不同的圆的交点最多有______个.
画2个圆,最多有2个交点,可以写成2×(2-1)个交点;
画3个圆,最多有6个圆,可以写成3×(3-1)个交点;
画4个大小不同的圆,最多有12个交点,可以写成是4×(4-1)个交点;…
所以画n个圆时,最多有n(n-1)个交点,
当n=5时,交点最多有:5×(5-1)=20(个),如图;
答:画7个大小不同的圆,最多有20个交点.
故答案为:20.
