问题
解答题
若∣m+4∣与n2-2n+1互为相反数,把多项式x2+4y2-mxy-n分解因式
答案
(x+2y+1)(x+2y-1)
由题意可得|m+4|+(n-1)2=0,
∴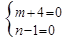 ,
,
解得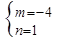 ,
,
∴x2+4y2-mxy-n,
=x2+4y2+4xy-1,
=(x+2y)2-1,
=(x+2y+1)(x+2y-1)
由题意可知|m+4|与n2-2n+1互为相反数,即|m+4|+(n-1)2=0,根据非负数的性质求出m=-4,n=1,再把m,n的值代入所求代数式利用分组分解法和完全平方公式、平方差公式分解因式即可.
