如图所示,相互平行的竖直分界面MN、PQ,相距L,将空间分为Ⅰ、Ⅱ、Ⅲ区.Ⅰ、Ⅲ区有水平方向的匀强磁场,Ⅰ区的磁感应强度未知,Ⅲ区的磁感应强度为B;Ⅱ区有竖直方向的匀强电场(图中未画出).一个质量为m、电荷量为e的电子,自MN上的O点以初速度v0水平射入Ⅱ区,此时Ⅱ区的电场方向竖直向下,以后每当电子刚从Ⅲ区进入Ⅱ区或从Ⅰ区进入Ⅱ区时,电场突然反向,场强大小不变,这个电子总是经过O点且水平进入Ⅱ区.(不计电子重力)
(1)画出电子运动的轨迹图;
(2)求电子经过界面PQ上两点间的距离;
(3)若Ⅱ区的电场强度大小恒为E,求Ⅰ区的磁感应强度.
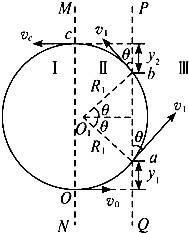
(1)电子运动的轨迹如图所示.
(2)电子在Ⅱ区Oa段做类平抛运动,
在a点的速度v1与PQ成θ角,v1sinθ=v0…①
电子在Ⅲ区ab段做匀速圆周运动,洛伦兹力提供向心力,有:
ev1B=
…②m v 21 R1
由几何知识有:
=2R1sinθ…③. ab
①②③联立解得:
=. ab
…④2mv0 eB
(3)电子在Ⅱ区Oa段运动的竖直位移:
y1=
at2=1 2
?(eE 2m
)2=L v0
…⑤eEL2 2m v 20
电子在bc段做类斜上抛运动,加速度与Oa段等值反向,由运动的对称性得
电子运动的竖直位移:
y2=y1=
…⑥eEL2 2m v 20
同样有对称可得电子在c处的速度为:
vc=v0,方向水平向左…⑦
所以,电子在Ⅰ区CO段做匀速圆周运动的半径为:
R′=
(y1+y2+1 2
)…⑧. ab
由牛顿运动定律有:
ev0B=
…⑨m v 20 R′
解得:
B′=
(或mv0
+mv0 B e2L2E 2Em v 20
)2m2
Bv 30 2m2
+e2L2BEv 30
答:(1)电子运动的轨迹图如图所示.
(2)电子经过界面PQ上两点间的距离为
.2mv0 eB
(3)若Ⅱ区的电场强度大小恒为E,Ⅰ区的磁感应强度为
.mv0
+mv0 B e2L2E 2Em v 20
