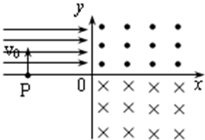
如图所示,在第二象限内有水平向右的匀强电场,电场强度为E;在第一、四象限内分别存在如图所示的匀强磁场,磁感应强度大小相等.有一个带电粒子以初速度v0从x轴上的P点垂直进入匀强电场,恰好与y轴45°角射出电场,再经过一段时间又恰好垂直于x轴进入下面的磁场.已知O、P之间的距离为d,则带电粒子( )
A.在电场中运动的时间为
d/v02
B.在磁场中做圆周运动的半径为
d2
C.自进入磁场至第二次经过x轴所用时间为7πd/4 v0
D.从进入电场时开始计时,粒子在运动过程中第二次经过x轴的时间为 (4+7π)d/2 v0
A、设带电粒子到达y轴Q点,Q点的纵坐标为h,到达Q点的水平分速度为vx,则由类平抛运动的规律可知
h=v0t
d=
vxt1 2
tan45°=vx v0
得h=2d,t=
故A错误.2d v0
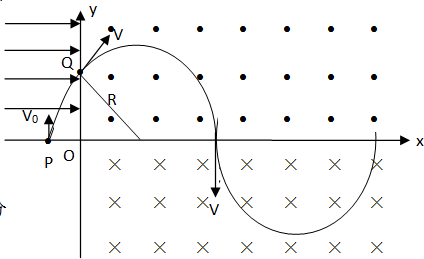
B、粒子在磁场中的运动轨迹如图所示,设粒子在磁场中运动的半径为R,周期为T.
则由几何关系可知:R=
h=22
d.故B错误.2
C、带电粒子进入磁场时的速度大小为 v=
v0 2
则粒子在磁场中运动的周期为 T=
=2πR v 4πd v0
粒子在磁场中的运动时间为t′
则t′=
T+3 8
T=1 2
T=7 8
.故C错误.7πd 2v0
D、从进入电场时开始计时,粒子在运动过程中第二次经过x轴的时间为t=t+t′=
+2d v0
=7πd 2v0
.故D正确.4+7πd 2v0
故选D
