问题
问答题
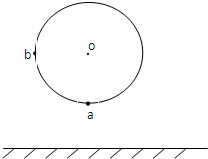
如图所示,半径为R的圆轮在竖直面内绕O轴匀速转动,轮边缘上的a、b两质点与O点的连线相互垂直,教a、b两质点均粘在轮边缘上,当a点转至如图的最低位置时,离地高度也为R,且a、b两质点同时脱落,经过相同时间落到水平地面上.
(1)求圆轮转动的角速度的大小.
(2)a、b两质点落到水平地面上的距离.
答案
(1)a、b两质点同时脱落,经过相同时间落到水平地面上,所以轮子做逆时针转动,a物体平抛,b物体竖直下抛,经过相同时间t落到水平地面上.
对平抛物体a竖直方向自由落体:R=
gt21 2
对竖直下抛的物体b:2R=vt+
gt21 2
解得:v=gR 2
由于v=ωR
得:ω=g 2R
(2)b的落地点在b物体的正下方,a物体做平抛运动,水平方向是匀速直线运动.
所以水平位移:x=vt
解得:x=R
所以a、b两质点落到水平地面上的距离为2R.
答:(1)求圆轮转动的角速度的大小
.g 2R
(2)a、b两质点落到水平地面上的距离为2R.
