问题
问答题
质谱仪的原理图如图甲所示.带负电粒子从静止开始经过电势差为U的电场加速后,从G点垂直于MN进入偏转磁场,该偏转磁场是一个以直线MN为上边界方向垂直于纸面向里的匀强磁场,磁场的磁感应强度为B,带电粒子经偏转磁场后,最终到达照片底片上的H点,测得G、H间的距离为d,粒子的重力可忽略不计.

(1)设粒子的电荷量为q,质量为m,试证明该粒子的比荷为:
=q m
;8U B2d2
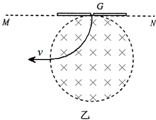
(2)若偏转磁场的区域为圆形,且与MN相切于G点,如图乙所示,其它条件不变,要保证上述粒子从G点垂直于MN进入偏转磁场后不能打到MN边界上(MN足够长),求磁场区域的半径应满足的条件.
答案
(1)粒子经过电场加速,进入偏转磁场时速度为v,
有qU=
mv2…①1 2
进入磁场后做圆周运动,设轨道半径为r,则有:r=
…②mv Bq
打到H点则:r=
…③d 2
解①②③得:
=q m 8U B2d2
(2)要保证所有粒子都不能打到MN边界上,粒子在磁场中偏转角度应小于或等于90°,偏转角度恰好等于90°的情况,如图所示,此时磁场区半径:R=r=d 2
所以,磁场区域半径应满足的条件为:R≤d 2
答:(1)证明见上.
(2)磁场区域的半径应满足的条件是R≤
.d 2
