问题
多选题
如图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使其在瞬间得到一个水平初速度v0,若v0大小不同,则小球能够上升到的最大高度(距离底部)也不同.下列说法中正确的是( )
A.如果v0=
,则小球能够上升的最大高度为gR R 2
B.如果v0=
,则小球能够上升的最大高度为2gR R 2
C.如果v0=
,则小球能够上升的最大高度为3gR 3R 2
D.如果v0=5gR,则小球能够上升的最大高度为2R 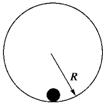
答案
A、如果v0=
,根据机械能守恒定律得:gR
mv02=mgh,解得:h=1 2
,当小球运动到R 2
高度时速度可以为零,则小球能够上升的最大高度为R 2
,故A正确,B错误;R 2
C、如果v0=
,根据机械能守恒定律得:3gR
mv02=mgh,解得:h=1 2
,当根据竖直平面内的圆周运动知识可知小球在上升到3R 2
处之前就做斜抛运动了,故C错误;3R 2
D、如果v0=
,根据机械能守恒定律得:5gR
mv02=mg?2R+1 2
mv2,解得v=1 2
,根据竖直方向圆周运动向心力公式可知,最高点的速度最小为gR
,gR
满足条件,所以可以到达最高点,即小球能够上升的最大高度为2R,故D正确.
故选AD