问题
问答题
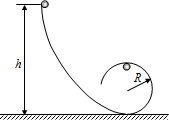
如图所示,质量为m的小球从光滑的离心轨道上由静止开始滑下后进入竖直面内的光滑圆形轨道,圆形轨道的半径为R,重力加速度为g,求:
(1)要使小球能通过圆形轨道的最高点,h至少应为多大?
(2)当h=4R时,小球运动到圆环的最高点时轨道对小球的弹力是多大?
答案
(1)设小球到达圆轨道最高点的最小速度为v,
小球恰好能通过圆轨道最高点有 mg=m
,v2 R
根据机械能守恒定律有 mgh=mg?2R+
mv2,1 2
解得 h=
,5R 2
故h至少应为
. 5R 2
(2)当h=4R时,设小球运动到圆环的最高点速度为v',
由机械能守恒定律得 mg?4R=mg?2R+
mv'2,1 2
在最高点有 mg+N=m
,v′2 R
解得 N=3mg.
答:(1)要使小球能通过圆形轨道的最高点,h至少应
.5R 2
(2)当h=4R时,小球运动到圆环的最高点时轨道对小球的弹力是3mg.
