问题
问答题
如图所示，空间分布着有理想边界的匀强电场和匀强磁场．左侧匀强电场的场强大小为E、方向水平向右，电场宽度为L；中间区域及右侧匀强磁场的磁感应强度大小均为B，方向垂直纸面向外和向里．一个质量为m、电量为q、不计重力的带正电的粒子从电场的左边缘的O点由静止开始运动，穿过中间磁场区域进入右侧磁场区域后，又回到O点，然后重复上述运动过程．要求：
（1）定性画出粒子运动轨迹，并求出粒子在磁场中运动的轨道半径R；
（2）中间磁场区域的宽度d；
（3）带电粒子从O点开始运动到第一次回到O点所用时间t．
答案
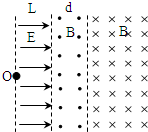
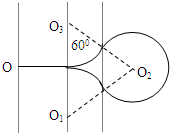
（1）粒子运动轨迹如图所示；
带电粒子在电场中加速，qEL=
mv21 2
带电粒子在磁场中偏转，Bqv=m
可得 R=v2 R 1 B
．2mEL q
（2）可见在两磁场区粒子运动半径相同，如图所示，三段圆弧的圆心组成的三角形△O1O2O3是等边三角形，其边长为2R．所以中间磁场区域的宽度为：d=Rsin60°=1 2B 6mEL q
（3）在电场中 t1=
=2v a
=22mv qE
，在中间磁场中运动时间t2=2mL qE
=T 3 2πm 3qB
在右侧磁场中运动时间t3=
=5T 6
，5πm 3qB
则粒子第一次回到O点的所用时间为
t=t1+t2+t3=2
+2mL qE 7πm 3qB
答：（1）粒子在磁场中运动的轨道半径R为1 B
；2mEL q
（2）中间磁场区域的宽度d为1 2B
；6mEL q
（3）带电粒子从O点开始运动到第一次回到O点所用时间为2
+2mL qE
．7πm 3qB