问题
问答题
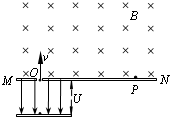
如图所示,MN表示真空室中垂直于纸面放置的感光板,它的一侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度大小为B;另一侧有一个匀强电强,电场方向平行于纸面向下,电场两极板间的电势差为U.一个电荷量为q、质量为m的带电粒子在电场一极板附近由静止释放,被电场直线加速,从感光板MN上的狭缝O处垂直射入磁场区域,最后到达感光板上的P点.不计带电粒子受到的重力.求:
(1)带电粒子垂直射入磁场区域时的速率v;
(2)P、O两点间的距离为l.
(3)如果要使得带电粒子到达感光板MN的P点距O点的距离增大,有哪些可行的方法?
答案
(1)带电粒子在电场中直线加速,电场力做功,动能增加,
由动能定理可知,
qU=
mv2,1 2
带电粒子垂直射入磁场区域时的速率为
v=2qU m
(2)带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力
由牛顿第二定律,则有qvB=m
,v2 R
几何关系,l=2R
解得P、O两点间的距离l=2 B 2mU q
(3)根据题意可知,若增大轨迹半径,可增大速率.由公式r=
,得可增大加速电压,从而提高速率.或降低磁场,则可增大半径.mv Bq
因此增大加速电场的电势差,或减小匀强磁场的磁感应强度,都可以带电粒子到达感光板MN的P点距O点的距离增大.
答:(1)带电粒子垂直射入磁场区域时的速率为v=
;2qU m
(2)P、O两点间的距离为l=2 B
.2mU q
(3)如果要使得带电粒子到达感光板MN的P点距O点的距离增大,可行的方法:增大加速电场的电势差,或减小匀强磁场的磁感应强度.
