在如图(a)所示的正方形平面oabc内存在着垂直于该平面向外的匀强磁场,磁感应强度大小为B,已知正方形边长为L.一个质量为m、带电量为+q的粒子(不计重力)在t=0时刻平行于oc边从o点射入磁场中.
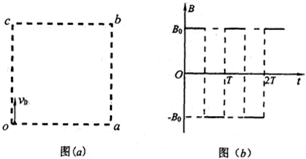
(1)若带电粒子从a点射出磁场,求带电粒子在磁场中运动的时间及初速度大小;
(2)若磁场的磁感应强度按如图(b)所示的规律变化,规定磁场向外的方向为正方向,磁感应强度的大小为B0,假使带电粒子能从oa边界射出磁场,求磁感应强度B变化周期T的最小值;
(3)若所加磁场与第(2)问中的相同,要使带电粒子从b点沿着ab方向射出磁场,求满足这一条件的磁感应强度变化的周期T及粒子射入磁场时的速度v0.
(1)若带电粒子从a点射出磁场,则做圆周运动的半径为r=L 2
所需时间t=
=T 2 πm qB
又根据m
=Bqv0v02 r
得v0=BqL 2m
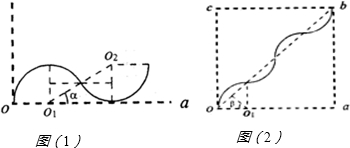
(2)要使粒子从oa边射出,其临界状态轨迹如图(1)所示
则有sinα=1 2
α=30°
在磁场变化的半个周期内,粒子在磁场中旋转150°角,运动时间t=
T0=5 12 5πm 6qB0
而t=T 2
所以磁场变化的最小周期为T=5πm 3qB0
(3)若使粒子从b点沿着ab方向射出磁场,轨迹如图(2).
在磁场变化的半个周期内,粒子在磁场中旋转的角度为2β,其中β=45°,
即
=T 2 T0 4
所以磁场变化的周期为T=πm qB0
每一个圆弧对应的弦长OM为s=
L(n=2,4,6…)2 n
圆弧半径r=
=s 2
(n=2,4,6…)L n
由m
=Bqv0,得v0=v02 r
(n=2,4,6…)BqL nm
(1)带电粒子在磁场中运动的时间为
及初速度大小为πm qB
;BqL 2m
(2)磁感应强度B变化周期T的最小值为
;5πm 3qB0
(3)满足这一条件的磁感应强度变化的周期T为
,粒子射入磁场时的速度v0为πm qB0
(n=2,4,6…).BqL nm
