问题
问答题
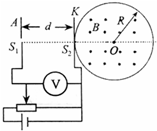
如图所示,所以O为圆心,R为半径的圆形区域内,有一个水平方向的匀强磁场,磁感应强度大小为B,方向垂直于纸面向外;竖直平行放置的极板A、K相距为d,AK之间的电压可以调节,S1、S2为A、K极板上的两个小孔,且S1、S2和O三点在垂直于极板的同一直线上,OS2=R;质量为m、电量为q的正离子从S1进入电场后,自S2射出并进入磁场区域,不计重力和离子进入电场时的初速度,问:
(1)为使正离子射出磁场时的速度的方向与进入时重直,A、K之间的电压应为多大?
(2)粒子在磁场中的运动时间多长?
答案
(1)正离子在电场中做初速度为零的加速直线运动
由动能定理得qU=
mv2①1 2
∵正离子以速度v进入匀强磁场,做匀速圆周运动Bqv=m
②v2 r
正离子离开磁场时的速度与进入时垂直,故r=R ③
解得A、K间的电压U=B2R2q 2m
(2)离子进入磁场后洛仑兹力提供向心力,由牛顿第二定律得:Bqv=m
④v2 R
离子在磁场中做匀速圆周运动的周期为:T=
⑤2πR v
离子在磁场中的运动时间为:t=
T⑥1 4
解④⑤⑥式得:t=πm 2Bq
答:(1)为使正离子射出磁场时的速度的方向与进入时重直,A、K之间的电压应为
;B2R2q 2m
(2)粒子在磁场中的运动时间为::t=
.πm 2Bq
