问题
问答题
（本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分。）
已知a∈R，函数=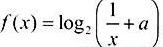
。
（1）当a=1时，解不等式f（x）>1；
（2）若关于x的方程f（x）+log2（x2）=0的解集中恰有一个元素，求a的值；
（3）设a>0，若对任意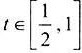
，函数f（x）在区间[t，t+1]上的最大值与最小值的差不超过1，求a的取值范围。
答案
参考答案：
解：（1）由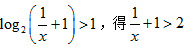
，解得x∈（0，1）。
（2）
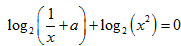有且仅有一解，等价于
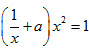有且仅有一解，等价于ax2+x-1=0有且仅有一解。
当a=0时，x=1，符合题意；
当a≠0时，△=1+4a=0，a=-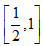
。
综上，a=0或-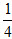
。
（3）当0<x1<x2时，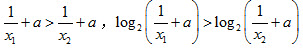
，所以f（x）在（0，+∞）上单调递减。
函数f（x）在区间[t，t+1]上的最大值与最小值分别为f（t），f（t+1）。
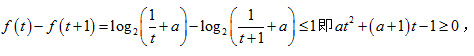对任意
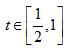成立。
因为a>0，所以函数y=at2+（a+1）t-1在区间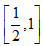上单调递增，t=
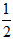时，y有最小值
。
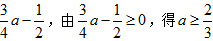故a的取值范围为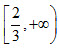
。
