问题
问答题
（本题共有2个小题，第1小题满分6分，第2小题满分8分。）
有一块正方形菜地EFGH，EH所在直线是一条小河，收获的蔬菜可送到F点或河边运走。于是，菜地分为两个区域S1和S2，其中S1中的蔬菜运到河边较近，S2中的蔬菜运到F点较近，而菜地内S1和S2的分界线C上的点到河边与到F点的距离相等。现建立平面直角坐标系，其中原点O为EF的中点，点F的坐标为（1，0），如图
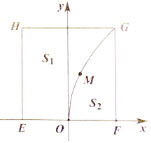
（1）求菜地内的分界线C的方程；
（2）菜农从蔬菜运量估计出S1面积是S1面积的两倍，由此得到S1面积的“经验值”为
。设M是C上纵坐标为1的点，请计算以EH为一边、另有一边过点M的矩形的面积，及五边形EOMGH的面积，并判别哪一个更接近于S1面积的“经验值”。
答案
参考答案：
解：（1）因为C上的点到直线EH与到点F的距离相等，所以C是以F为焦点、以EH为准线的抛物线在正方形EFGH内的部分，其方程为y2=4x（0<y<2）。
（2）依题意，点M的坐标为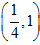
。
所求的矩形面积为
，而所求的五边形面积为
。
矩形面积与“经验值”之差的绝对值为
，而五边形面积与“经验值”之差的绝对值为
，所以五边形面积更接近于S1面积的“经验值”。