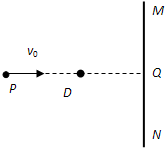
如图所示,MN为纸面内竖直放置的挡板,P、D是纸面内水平方向上的两点,两点距离PD为L,D点距挡板的距离DQ为
.一质量为m、电量为q的带正电粒子在纸面内从P点开始以v0的水平初速度向右运动,经过一段时间后在MN左侧空间加上垂直纸面向里的磁感应强度为B的匀强磁场,磁场维持一段时间后撤除,随后粒子再次通过D点且速度方向竖直向下.已知挡板足够长,MN左侧空间磁场分布范围足够大.粒子的重力不计.求:L π
(1)粒子在加上磁场前运动的时间t;
(2)满足题设条件的磁感应强度B的最小值及B最小时磁场维持的时间t0的值.
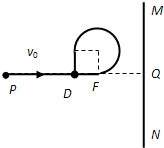
(1)微粒从P点至第二次通过D点的运动轨迹如图所示
由图可知在加上磁场前瞬间微粒在F点(圆和PQ的切点).
在t时间内微粒从P点匀速运动到F点,t=
…①PF v0
由几何关系可知:PF=L+R… ②
又 R=
…③mv0 Bq
由①②③式可得:t=
+L v0 m Bq
(2)微粒在磁场中作匀速圆周运动时,由②式可知:当R最大时,B最小,在微粒不飞出磁场的情况下,R最大时有:
DQ=2R,
即
=2RL π
可得B的最小值为:Bmin=2πmv0 qL
微粒在磁场中做圆周运动,故有t0=(n+
)T,n=0,1,2,3,3 4
又:T=2πm Bq
即可得:t0=
,(n=0,1,2,3,…)(n+
)L3 4 v0
答:(1)粒子在加上磁场前运动的时间t为
+L v0
;m Bq
(2)满足题设条件的磁感应强度B的最小值为
,B最小时磁场维持的时间t0为2πmv0 qL
,(n=0,1,2,3,…).(n+
)L3 4 v0
