问题
问答题
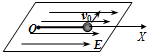
如图所示,沿X方向存在一匀强电场,现在光滑绝缘的水平面上有一长为l的绝缘细线,细线一端系在坐标原点O,另一端系一质量为m、带电量为+q的小球,此时小球保持静止.现给小球一垂直于细线的很小的初速度v0,使小球在水平面上开始运动,若小球在X方向发生最大的位移大小为△x,求匀强电场的场强E大小和小球第一次到达电势能最大的位置所需的时间t.
某同学对小球运动分析和求解如下:
①给小球一垂直于细线的初速度v0后,小球作匀速圆周运动,电场力作为向心力,由向心力公式可解出场强;
②由运动学公式△x=
at2可求得时间t.1 2
请说明该同学的解题思路是否正确?如有错误,请指出错处,并作出正确解答;如果正确,请完成解答.
答案
小球获得初速度后水平方向受到电场力和绳子的拉力,电场力是恒力,合外力并不指向圆心,不可能作匀速圆周运动,电场力不可能作为向心力,因而场强的解答是错误的;
运动学公式 △x=
at2只适用于匀加速直线运动,而小球作变加速曲线运动,因而时间t求解错误. 1 2
正确解答是:在X方向运用动能定理得:Eq△x=
m1 2 v 2o
得场强 E=m v 2o 2q△x
由于是匀强电场,电场力为恒力,小球获得很小的初速度后在绳拉力和电场力的共同作用下将作简谐振动,小球第一次到达电势能最大的位置所需的时间为
周期,1 4
△t=
=T 4 π 2
=lm Eq π 2
=2△xl v 2o π vo △xl 2
答:该同学的解题思路是错误的.匀强电场的场强E大小为
,小球第一次到达电势能最大的位置所需的时间t为m v 2o 2q△x π vo
.△xl 2
