问题
问答题
（本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分。）
对于无穷数列{an}与{bn}，记A={x|x=an，n∈N*}，B={x|x=bn，n∈N*}，若同时满足条件：①{an}，{bn}均单调递增；②A∩B=
且A∪B=N*，则称{an}与{bn}是无穷互补数列。
（1）若an=2n-1，bn=4n-2，判断{an}与{bn}是否为无穷互补数列，并说明理由；
（2）若an=2n且{an}与{bn}是无穷互补数列，求数列{bn}的前16项的和；
（3）若{an}与{bn}是无穷互补数列，{an}为等差数列且a16=36，求{an}与{bn}的通项公式。
答案
参考答案：
解：（1）因为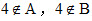
，所以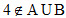
，
从而{an}与{bn}不是无穷互补数列。
（2）因为a4=16，所以b16=16+4=20。
数列{bn}的前16项的和为
。
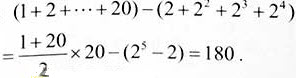（3）设{an}的公差为d，d=∈N*，则a16=a1+15d=36。
由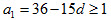
，得d=1或2。
若d=1，则a1=21，an=n+20，与“{an}与{bn}是无穷互补数列”矛盾；
若d=2，则a1=6，an=2n+4，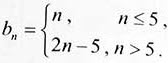
。
综上，an=2n+4，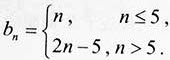
。