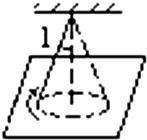
如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当把绳子拉直时,绳子与竖直线夹角为60°,此时小球静止于光滑水平桌面上.
(1)当球以ω=
做圆锥摆运动时,绳子张力T为多大?桌面受到压力N为多大?g l
(2)当球以角速度ω=
做圆锥摆运动时,绳子的张力及桌面受到的压力各为多少?4g l
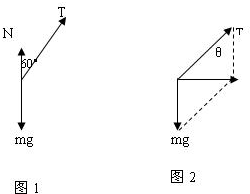
(1)对小球受力分析,作出力图如图1.
根据牛顿第二定律,得
Tsin60°=mω2Lsin60°①
mg=N+Tcos60° ②
又ω=g l
解得
T=mg,N=
mg1 2
(2)设小球对桌面恰好无压力时角速度为ω0,即N=0
代入①②得ω0=2g L
由于ω=
>ω0,故小球离开桌面做匀速圆周运动,则N=0此时小球的受力如图2.设绳子与竖直方向的夹角为θ,则有4g l
mgtanθ=mω2?Lsinθ③
mg=Tcosθ ④
联立解得 T=4mg
答:
(1)当球以ω=
做圆锥摆运动时,绳子张力T=mg,桌面受到压力N=g l
mg;1 2
(2)当球以角速度ω=
做圆锥摆运动时,绳子的张力为4mg,桌面受到的压力为零.4g l