问题
问答题
（本题共有2个小题，第1小题满分6分，第2小题满分8分。）
双曲线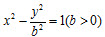
的左、右焦点分别为F1、F2，直线l过F2且与双曲线交于A、B两点。
（1）若l的倾斜角为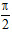
，△F1AB是等边三角形，求双曲线的渐近线方程；
（2）设b=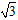
，若l的斜率存在，且|AB|=4，求l的斜率。
答案
参考答案：
解：（1）设A（xA，yA）。
由题意，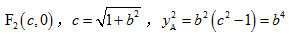
，
因为△F1AB是等边三角形，所以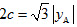
，
即4（1+b2）=3b4，解得b2=2。
故双曲线的渐近线方程为
。
（2）由已知，F2（2，0）。
设A（x1，y1），B（x2，y2），直线l：y=k（x-2）。
由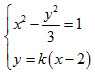
，得（k2-3）x2-4k2x+4k2+3=0。
因为l与双曲线交于两点，所以k2-3≠0，且△=36（1+k2）>0。
解得k2=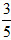
，故l的斜率为
。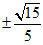