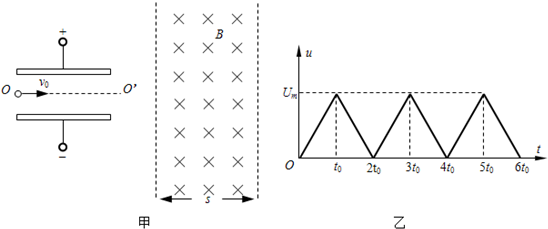
如图甲所示,水平放置的两平行金属板间距离为d,板长为l,OO′为两金属板的中线.在金属板的右侧有一竖直宽度足够大的匀强磁场,其左右边界均与OO′垂直,磁感应强度的大小为B,方向垂直纸面向里.两金属板间的电压u随时间t变化的图象如图乙所示.现有质子连续不断地以速度v0沿两金属板的中线射入电场中,每个质子在电场区域运动的时间内可以认为两金属板间的电场强度不变,已知质子的质量为m、电荷量为e.
(1)若在t=0时射入的质子能从磁场左边界飞出,试求质子在磁场中运动的时间t1;
(2)若射入的质子都能飞出电场,试求两金属板间所加电压的最大值Um;
(3)在(2)的情况下,为使由电场飞出的质子均不能从磁场右边界飞出,则匀强磁场的水平宽度s应满足什么条件?
解
(1)t=0时场强为0,质子在在极板间不偏转.
质子在磁场中做圆周运动的周期T=2πm Be
质子在磁场中运动了半个周期,所以t1=πm Be
(2)质子在电场中做类平抛运动,由运动学公式,则有
y═
=d 2
at2=1 2 1 2
(Ume md
)2l v0
解得:Um=md2 v 20 el2
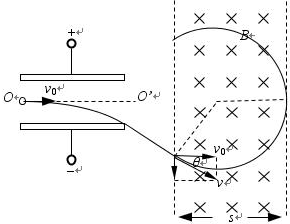
(3)
根据运动的分解,则有速度关系,v=v0 cosθ
因运动半径公式,r=
=mv Be mv0 Becosθ
又几何关系,s0=r+rsinθ
质子就好像从O O′飞出电场一样
则tanθ=
=d 2 l 2 d l
所以s0=mv0(d+
)l2+d2 eBl
则应满足的条件为s=mv0(d+
)l2+d2 eBl
答:(1)若在t=0时射入的质子能从磁场左边界飞出,则质子在磁场中运动的时间t1=
;πm Be
(2)若射入的质子都能飞出电场,则两金属板间所加电压的最大值:Um=
;md2 v 20 el2
(3)在(2)的情况下,为使由电场飞出的质子均不能从磁场右边界飞出,则匀强磁场的水平宽度应满足s=
条件.mv0(d+
)l2+d2 eBl
