问题
问答题
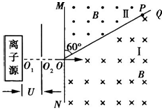
如图所示,在NOQ范围内有垂直于纸面向里的匀强磁场I,在MOQ范围内有垂直于纸面向外的匀强磁场Ⅱ,M、O、N在一条直线上,∠MOQ=60°,这两个区域磁场的磁感应强度大小均为B.离子源中的离子带电荷量为+q,质量为m,通过小孔O1进入两板间电压为U的加速电场区域(可认为初速度为零),离子经电场加速后由小孔O2射出,再从O点进入磁场区域I,此时速度方向沿纸面垂直于磁场边界MN不计离子的重力.
(1)若加速电场两板间电压U=U0,求离子进入磁场后做圆周运动的半径R0
(2)在OQ上有一点P,P点到O点距离为若离子能通过P点,求加速电压U和从O点到P点的运动.
答案
(1)离子在电场中加速时,根据动能定理得

qU0=
m1 2 v 20
电子在磁场中运动时,由洛伦兹力提供向心力,则有
qv0B=mv 20 R0
联立解得,R0=1 B 2U0m q
(2)离子进入磁场时的运动轨迹如图所示,由几何关系可知
=. OP′
=R0. P′P″
要保证离子通过P点,必须有 L=nR
解得,U=
其中n=1,2,3,…B2L2q 2mn2
又离子运动的周期为 T=2πm qB
则离子从O点到P点的运动时间为 t=n?
?T=π 3 2π
,其中n=1,2,3,…nπm 3qB
答:(1)离子进入磁场后做圆周运动的半径R0为1 B
.2U0m q
(2)加速电压U是
其中n=1,2,3,…,离子从O点到P点的运动时间为B2L2q 2mn2
,其中n=1,2,3,….nπm 3qB
