问题
问答题
(本题共有2个小题,第1小题满分6分,第2小题满分6分。)
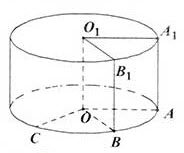
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,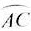 长为
长为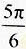 ,
,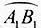 长为
长为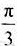 ,其中B1与C在平面AA1O1O的同侧。
,其中B1与C在平面AA1O1O的同侧。
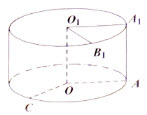
(1)求圆柱的体积与侧面积;
(2)求异面直线O1B1与OC所成的角的大小。
答案
参考答案:
解:(1)由题意可知,圆柱的母线长l=1,底面半径r=1。
圆柱的体积V=πr2l=π×12×1=π,
圆柱的侧面积S=2πrl=2π×1×1=2π。
(2)设过点B1的母线与下底面交于点B,则O1B1∥OB,
所以∠COB或其补角为O1B1与OC所成的角。
由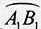 长为
长为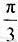 ,可知∠AOB=∠A1O1B1=
,可知∠AOB=∠A1O1B1=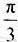 ,
,
由长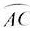 为
为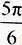 ,可知∠AOC=
,可知∠AOC=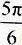 ,∠COB=∠AOC-∠AOB=
,∠COB=∠AOC-∠AOB=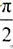 ,
,
所以异面直线O1B1与OC所成的角的大小为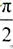 。
。