问题
问答题
如图所示,将长为L的绝缘细线的一端固定定在O点,另一端系一质量为m,带电量为q的带正电的小球,使小球在水平面内做匀速圆周运动(圆锥摆),线和竖直方向的夹角为,重力加速度为g.
(1)求小球圆周运动的速率.
(2)求线的拉力大小.
(3)若某时刻突然加一竖直向上的场强E=mg/q的匀强电场之后,求线的拉力大小.

答案
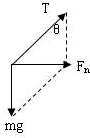
(1)以小球为研究对象,作出力图如图.设小球圆周运动的速率为v,则有
mgtanθ=mv2 Lsinθ
解得 v=gLtanθsinθ
(2)由力图得,线的拉力大小T=mg cosθ
(3)若突然加一竖直向上的场强E=
的匀强电场之后,电场力与重力平衡,小球将以原来的速率、O点为圆心在水平面内做匀速圆周运动,由细线的拉力提供向心力,则由牛顿第二定律得mg q
T=m
=mgtanθsinθv2 L
答:
(1)小球圆周运动的速率为
.gLtanθsinθ
(2)线的拉力大小是
.mg cosθ
(3)若某时刻突然加一竖直向上的场强E=
的匀强电场之后,线的拉力大小为mgtanθsinθ.mg q
