问题
问答题
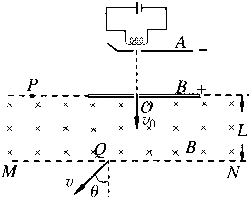
在水平放置的两块金属板AB上加不同电压,可以使从炽热的灯丝释放的电子以不同速度沿直线穿过B板中心的小孔O进入宽度为L的匀强磁场区域,匀强磁场区域的磁感应强度为B,方向垂直纸面向里.若在A、B两板间电压为UO时,电子不能穿过磁场区域而打在B板延长线上的P点,如图所示.已知电子的质量为m,电荷量为e,并设电子离开A板时的初速度为零.
(1)求A、B两板间的电压为U0时,电子穿过小孔O的速度大小v0;
(2)求P点距小孔D的距离x;
(3)若改变A、B两板间的电压,使电子穿过磁场区域并从边界MN上的Q点射出,且从Q点穿出时速度方向偏离v0方向的角度为θ,则AB两板间电压U为多大?
答案
(1)电子在AB板间电场中加速时,由动能定理得:
eU0=
m1 2
解得v0=v 20 2eU0 m
(2)电子进入磁场区域做匀速圆周运动,由牛顿第二定律可得
ev0B=mv 20 R
解得 R=1 B 2mU0 e
故x=2R=2 B
.2mU0 e
(3)若在A、B两板间加上电压U时,电子在AB板间加速后穿过B板进入磁场区域做圆周运动,并从边界MN上的Q点穿出,由动能定理可得
eU=
mv21 2
由牛顿第二定律可得 evB=mv2 r
由几何关系可知 rsinθ=L
综上所得U=
.eB2L2 2msin2θ
答:(1)当A、B两板间的电压为U0时,电子穿过小孔O的速度大小v0=
.2eU0 m
(2)P点距小孔D的距离x=2 B
.2mU0 e
(3)AB两板间电压U=
.eB2L2 2msin2θ
