问题
选择题
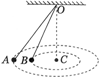
如图所示,两根长度不同的细绳,一端固定于O点,另一端各系一个相同的小铁球,两小球恰好在同一水平面做圆周运动,则( )
A.它们做圆周运动的频率相等
B.它们所需的向心力跟轨道半径成反比
C.它们做圆周运动的线速度大小相等
D.B球受绳的拉力较大
答案
A、设绳子与竖直方向的夹角为θ,则有mgtanθ=mlsinθω2.解得ω=
,两球的竖直高度相同,即lcosθ相同,则角速度相同,根据f=g lcosθ
,知频率相同.故A正确.ω 2π
B、向心力等于合外力,即F向=mgtanθ=mg
.与r成正比.故B错误.r h
C、圆周运动的线速度v=rω,角速度相同,半径不同,则线速度不等.故C错误.
D、小球在竖直方向上的合力等于零,有mg=Tcosθ.T=
.知A球受绳子的拉力较大.故D错误.mg cosθ
故选A.

