问题
问答题
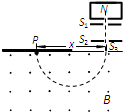
如图所示为一质谱仪的构造原理示意图,整个装置处于真空环境中,离子源N可释放出质量均为m、电荷量均为q(q>0)的离子.离子的初速度很小,可忽略不计.离子经S1、S2间电压为U的电场加速后,从狭缝S3进入磁感应强度大小为B、方向垂直于纸面向外的匀强磁场中,沿着半圆运动到照相底片上的P点处,测得P到S3的距离为x.求:
(1)离子经电压为U的电场加速后的速度v;
(2)离子的荷质比 (q/m)
答案
(1)离子经S1、S2间电压为U的电场加速,根据动能定理
qU=
mv2 得v=1 2
①2qU m
(2)设离子进入磁场后做匀速圆周运动速率为v,半径为R.
由洛伦兹力提供向心力得,qvB=
②mv2 R
又因 R=
x ③1 2
联立①②③,解得
=q m 8U B2x2
答:(1)离子经电压为U的电场加速后的速度得v=
;2qU m
(2)离子的荷质比
=q m
.8U B2x2
