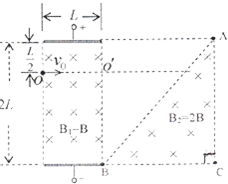
如图所示,平行板电容器板长为L,极板间距为2L,上板带正电,忽略极板外的电场. O、O′是电容器的左右两侧边界上的点,两点连线平行于极板,且到上极板的距离为L/2. 在电容器右侧存在一个等腰直角三角形区域ABC,∠C=90°,底边BC与电容器的下极板共线,B点与下极板右边缘重合,顶点A与上极板等高. 在电容器和三角形区域内宥垂直纸面向里的匀强磁场,磁感应强度大小分别为B1=B、B2=2B.一带正电的粒子以初速度v0从O点沿着00′方向射入电容器,粒子的重力和空气阻力均不计.
(1)若粒子沿 00′做直线运动,进人三角形区域后,恰从顶点 A飞出,求两极板间的电压U和带电粒子的比荷
.q m
(2)若撤去电容器中磁场的同时,把三角形区域内的磁场方向变为垂直于纸面向外,但磁感应强度大小不变.此后,同一带电粒子仍以相同的初速度v0 从0点沿着 00′方向射入电容器,求粒子从三角形区域飞出时距离飞出边某一顶点的距离.
(1)粒子在电容器中受力平衡,故:
q=Bqv0①U 2L
由于三角形区域ABC为等腰直角三角形,故粒子进入磁场B2到从A射出的轨迹为
圆周,故半径:1 4
R1=
②L 2
洛伦兹力提供向心力,由牛顿第二定律得:
2Bqv0=
③mv 20 R1
由以上得,
=q m
④v0 BL
(2)粒子在电容器中做类平抛运动,设飞出电场时侧向位移为y,速度方向偏转角为θ,则有:
y=
×1 2
×(Uq 2Lm
)2⑤L v0
tanθ=
=y L 2
⑥2y L
解①④⑤⑥得:y=
,θ=45°⑦L 2
速度大小为:v=
v0⑧2
粒子射出电场后进入磁场前做匀速直线运动,故将垂直于AB边进入磁场,且做顺时针偏转,设半径为R2,则有:
2Bqv=
⑨mv2 R2
由②③④⑧⑨得:R2=
L2 2
由于粒子垂直于AB边进入磁场,且∠ABC=45°,故应垂直于BC边射出,故出射点到B点的距离为:
x=R2=
L2 2
答:(1)带电粒子的比荷
为q m v0 L
(2)出射点到B点的距离为
L2 2
