如图,带电量为+q、质量为m的粒子(不计重力)由静止开始经A、B间电场加速后,沿中心线匀速射入带电金属板C、D间,后粒子由小孔M沿径向射入一半径为R的绝缘筒,已知C、D间电压为U0,板间距离为d,C、D间与绝缘筒内均有垂直于纸面向里的匀强磁场,磁感应强度分别为B0、B.
(1)求粒子在C、D间穿过时的速度v0;
(2)求A、B间的加速电压U;
(3)粒子与绝缘筒壁碰撞,速率、电荷量都不变,为使粒子在筒内能与筒壁碰撞4次(不含从M孔出来的一次)后又从M孔飞出,求筒内磁感应强度B (用三角函数表示).

(1)∵粒子在C、D间做匀速运动,则:
Eq=B0qv0 而E=
有:粒子在C、D间的速度v0=U0 d U0 dB0
(2)粒子在A、B间加速过程有:qU=
m1 2
在C、D间匀速运动有:qE=qv0B0v 20
且E=U0/d 解得:U=m U 20 2q
d2B 20
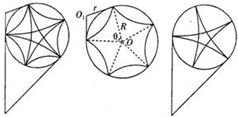
(3)带电离子在圆形磁场中运动的可能轨迹如图:
由(1)得:v0=U0 B0d
离子在圆形磁场中有:qv0B=m
.v 20 r
所以B=
=mv0 qr mU0 B0dqr
如图所示:r=Rtan
由几何知识易知:5θ=2nπ,n=1或2 θ 2
第一种情况:θ=
,则r=Rtan2π 5
,所以B=π 5
=mU0 B0dqr mU0 qB0dRtan(
)π 5
第二种情况:θ′=
,4π 5
则r′=Rtan
,B=2π 5 muo qB0dRtan(
)2π 5
答:(1)粒子的速度为V0=U0 dB0
(2)A、B间的加速电压为U= mU02 2qB02d2
(3)可能的运动轨迹如图所示,对应的B为
或mu0 qB0dRtan(
)π 5
.mU0 qB0dRtan(
)2π 5
